Кинематика тела
Различные виды движения твёрдого тела.
Различают пять видов движения:
• поступательное;
• вращательное - вокруг неподвижной оси;
• плоское;
• вокруг неподвижной точки;
• свободное.
Поступательное движение и вращательное движение вокруг оси - основные виды движения твердого тела. Остальные виды движения твердого тела можно свести к одному из этих основных видов или к их совокупности.
Поступательное - это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе и все точки твердого тела совершают равные перемещения за одинаковое время (рис. 2.12).
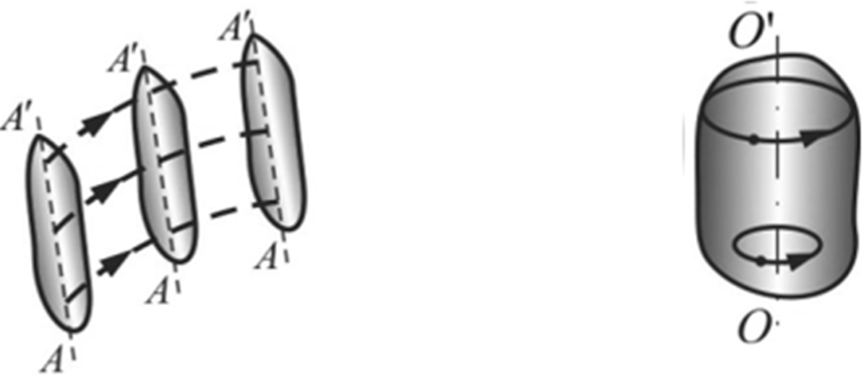
Рис. 2.12. Поступательное движение Рис. 2.13. Вращательное движение тела тела
При вращательном движении вокруг оси все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью ОО' вращения (рис. 2.13). Из определения вращательного движения ясно, что понятие вращательного движения для материальной точки неприемлемо.
Вращательное движение вокруг неподвижной оси
Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения.
Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО'(рис. 2.14).
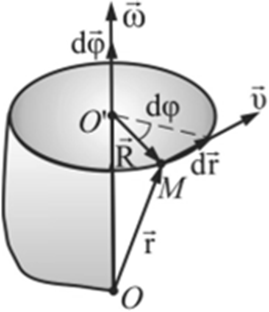
Рис. 2.14. Вращательное движение твердого тепа вокруг оси ОО'
Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr.
При том же самом угле поворота dtp другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого
dr d2r
тела, ни первая производная —, ни вторая производная —=- не могут
dt dr
служить характеристикой движения всего твердого тела.
За это же время dt радиус-вектор R, проведенный из точки О’ в точку М, повернется на угол dtp. На такой же угол повернется радиус- вектор любой другой точки (т. к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).
Угол поворота dtp характеризует перемещение всего тепа за время d/.
Удобно ввести dtp - вектор элементарного поворота тела, численно равный dtp и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора dtp и направление вращения связаны «правилом буравчика»).
Мгновенный центр скоростей.
Мгновенным центром скоростей (или мгновенным центром вращения) называют ту точку плоской фигуры, скорость которой в данный момент времени равна нулю. Покажем, что если угловая скорость фигуры отлична от нуля (со Ф 0), то такая точка существует и единственна.
Пусть в некоторый момент времени известна скорость А точки А фигуры и угловая скорость фигуры со Ф 0.
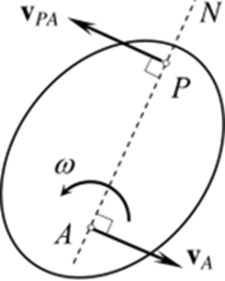
Рис. 8.8
Проведем прямую AN, перпендикулярную вектору Уд, и отложим на ней (рис. 8.8) отрезок
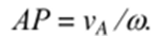
Найдем скорость точки Р фигуры при помощи векторной формулы (8.4):
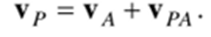
Оба вектора в правой части этого равенства перпендикулярны к AN, т.с. параллельны друг другу, и направлены в противоположные стороны (рис. 8.8). Модули их равны, т.к. согласно (8.5)
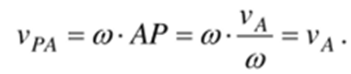
Поэтому vр = ул + уРд = 0, следовательно, точка Р является мгновенным центром скоростей (МЦС) фигуры. Единственность МЦС следует из процедуры его построения.
Пусть точка Р - мгновенный центр скоростей плоской фигуры, тогда скорость любой точки фигуры выражается в виде
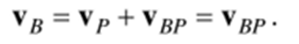
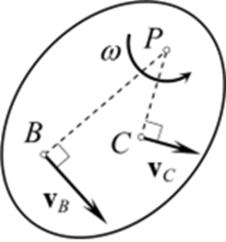
Рис. 8.9
Здесь ВР - это вектор скорости точки В при вращении фигуры вокруг центра Р с угловой скоростью со, вектор в = ВР направлен перпендикулярно отрезку РВ в сторону вращения фигуры (рис. 8.9), а его величина согласно (8.5)
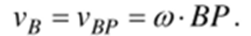
Это значит, что скорость любой точки фигуры находится так, как если бы фигура вращалась в своей плоскости с угловой скоростью со вокруг МЦС (рис. 8.9).
Из равенств vB = со ? ВР и vc = со- СР следует пропорция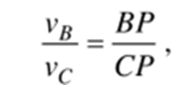
т.е. величина скорости точки плоской фигуры пропорциональна её расстоянию от МЦС.
Для решения задач кинематики плоского движения удобно пользоваться следующими правилами построения МЦС.
Абсолютная скорость.
Определение абсолютной скорости точки
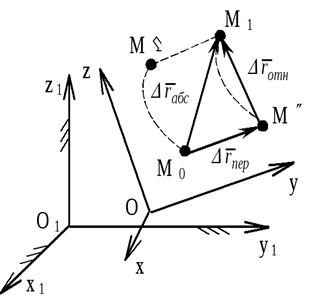
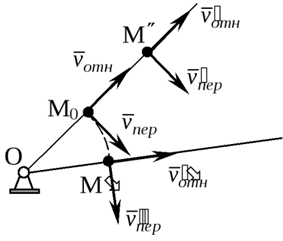
Рассмотрим
точку, совершающую сложное движение. Для нее будет справедливо выражение
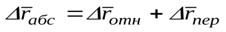
Разделим (48) на Dt и перейдем к пределу, в итоге получим
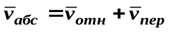
Уравнение (49) выражает следующую теорему.
Теорема: Абсолютная скорость точки, совершающей сложное движение, равна геометрической сумме относительной и переносной скоростей.
Модуль абсолютной скорости можно найти по теореме косинусов
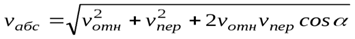
где a – угол между векторами 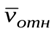 и
и 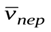
Определение абсолютного ускорения точки
Возьмем векторную производную от (49)
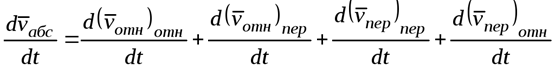
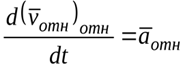 -относительное
ускорение
-относительное
ускорение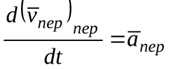 переносное
ускорение;
переносное
ускорение;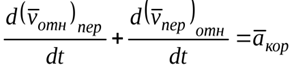 поворотное
ускорение Кориолиса, характеризующее изменение относительной скорости в
переносном движении и переносной скорости в относительном движении.
поворотное
ускорение Кориолиса, характеризующее изменение относительной скорости в
переносном движении и переносной скорости в относительном движении.В итоге уравнение (50) принимает вид
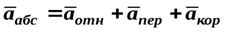
Уравнение (51) выражает следующую теорему Кориолиса.
Теорема: Абсолютное ускорение материальной точки по величине и направлению определяется геометрической суммой относительного ускорения, переносного ускорения и кориолисова ускорения.
Кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную линейную скорость
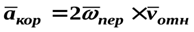
Если угол между векторами
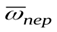 и
и 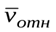 равенa, то
равенa, то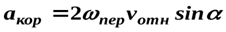
Направлен вектор кориолисова ускорения перпендикулярно плоскости, проходящей через векторы
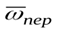 и
и 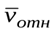 в ту
сторону, откуда совмещение на кратчайший угол
в ту
сторону, откуда совмещение на кратчайший угол 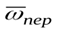 и
и 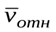
наблюдается происходящим против хода часовой стрелки.
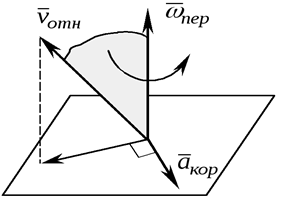
Из уравнения (53) следует, что кориолисово ускорение обращается в ноль, когда:
1. 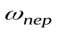 =0,
переносное движение - поступательное,
=0,
переносное движение - поступательное,
2. 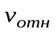 =0
=0
3. a.=0 или a=p, относительное движение происходит по направлению параллельному оси переносного вращения.