Основные понятия и аксиомы динамики

Динамика.

Динамика — это раздел теоретической механики, в котором изучается движение материальных тел, объектов и механических систем с учетом причин, вызывающих это движение. Эти причины называются силами.

Происхождение сил в механике не рассматривается, а изучается только их действие на движущиеся объекты. В отличие от статики в динамике как активные силы, так и реакции связей могут быть переменными.

При решении конкретных задач динамики свойства материальных объектов схематизируют, принимая во внимание наиболее существенные из этих свойств.

Простейшей схематизацией материального тела, является материальная точка, которая представляет собой тело определенной массы, положение которого можно определить как положение геометрической точки.

В теоретической механике все тела рассматриваются как совокупность взаимодействующих материальных точек. Такая совокупность называется механической системой материальных точек.

В динамике рассматривают следующие две основные задачи:

по заданному закону движения данной материальной точки определить действующие на эту точку силы;

зная силы, действующие на данную материальную точку, определить закон ее движения.

При решении этих задач используются установленные в статике способы приведения сил и разработанные в кинематике методы описания и изучения движения.

Основные понятия и аксиомы динамики.

Аксиомы динамики

Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную этих законах, называют классической механикой.

Первая аксиома (принцип инерции)

Всякая изолированная материальная точка находится в со­стоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.

Это состояние называют состоянием инерции. Вывести точку из этого состояния, т.е. сообщить ей некоторое ускорение, может внешняя сила.

Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела.

Массой называют количество вещества в объеме тела, в клас­сической механике ее считают величиной постоянной. Единица из­мерения массы — килограмм (кг).

Вторая аксиома (второй закон Ньютона — основной закон динамики)

Зависимость между силой, действующей на материальную точ­ку, и сообщаемым ею ускорением следующая: F = ma

где m — масса точки, кг;

а — ускорение точки, м/с².

Ускорение, сообщенное материальной точке силой, пропорци­онально величине силы и совпадает с направлением силы.

Основной закон динамики в дифференциальной форме:

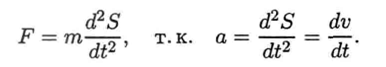
На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли: 

где g = 9,81 м/с², ускорение свободного падения.

Третья аксиома (третий закон Ньютона)

Силы взаимодействия двух тел равны по величине и направле­ны по одной прямой в разные стороны (рис. 1.12.1):

 

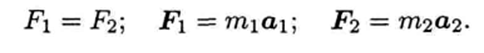
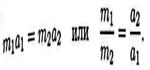
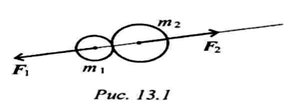
Откуда  m₁a_{1 =} m₂a₂ 

При взаимодействии ускорения обратно пропорциональны мас­сам.

Четвертая аксиома (закон независимости действия сил) Каждая сила системы сил действует так, как она действовала бы одна.

Ускорение, сообщаемое точке системой сил, равно геометриче­ской сумме ускорений, сообщенных точке каждой силой в отдельно­сти (рис. 1.12.2):

Рисунок 2.

Понятия о силе инерции.

Инерция (от лат. inertia — бездеятельность, косность) — свойство тел сохранять покой или равномерное прямолинейное движение, если внешние воздействия на него отсутствуют или взаимно скомпенсированы.

Сила инерции, векторная величина, численно равная произведению массы т материальной точки на ее ускорение w и направленная противоположно ускорению. При криволинейном движении С. и. можно разложить на касательную, или тангенциальную составляющую Jt направленную противоположно касательному ускорению wt, и на нормальную, или центробежную составляющую Jn, направленную вдоль главной нормали к траектории от центра кривизны; численно Jt = nwt, Jn = mv2/r, где v — скорость точки, r — радиус кривизны траектории.

Принцип Даламбера — в механике: один из основных принципов динамики, согласно которому, если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил.

Метод кинетостатики.

В технических задачах, не связанных с необходимостью интегрирования дифференциальных уравнений движения материальных объектов, иногда удобно пользоваться так называемым методом кинетостатики. Этот метод наиболее употребителен в случаях, когда требуется в постановке прямой задачи динамики определить неизвестную часть сил (как правило, силы реакции), участвующих в движении материального объекта.

Метод кинетостатики позволяет решать задачи динамики (неравномерного движения) методом статики. Для этой цели инерционные члены, стоящие в левой части дифференциальных уравнений переносятся в правую часть и их рассматривают как условные силы или условные моменты. Метод кинетостатики в своей основе предложил Даламбер и эти условные силы и условные моменты называют:

- силами инерции Даламбера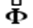 
- моментами сил инерции Даламбера 

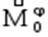
Рассмотрим применение метода кинетостатики (принципа Даламбера) для материальной точки и механической системы.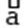

Следовательно можно записать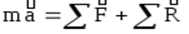 

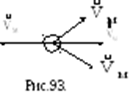 Перенесём инерционный член  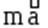в правую часть. Получим: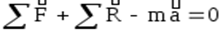

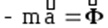Обозначим  таким образом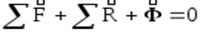 

Уравнение (1) по своему характеру является уравнением равновесия сил и может быть решено методами статики. Замечаем, что условно введённая сила инерции направлена по линии ускорения в противоположную сторону.

Сформулируем метод кинетостатики для материальной точки:

При неравномерном движении материальной точки в каждый момент времени геометрическая сумма задаваемых сил, сил реакции связей и силы инерции, условно приложенной к точке, взаимно уравновешена(равна нулю).

Обычно векторное уравнение (1) записывают в проекциях на оси координат, например:

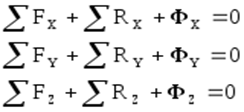
§ 2. Метод кинетостатики для твёрдых тел и механической системы.

а) При поступательном движении твёрдого тела

Как известно, поступательное движение тела описывается одним векторным уравнением, полученным на основе теоремы о движении центра масс:

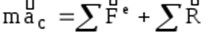
Выполним переход Даламбера, обозначив 

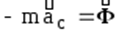
Таким образом:

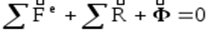
Или в проекциях на оси координат:

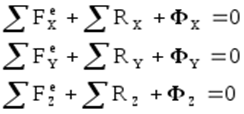
Получим: При неравномерном поступательном движении тела в каждый момент времени геометрическая сумма внешних сил, сил реакции связей и силы инерции, условно приложенной в центре масс, взаимно уравновешена.

б) При вращательном движении твёрдого тела.

Рассмотрим наиболее общий случай неравномерного вращения тела относительно неподвижной оси Z, не проходящей через центр тяжести. Пусть вращение характеризуется величинами w_z и e _z ; расстояние между точками О и С равно d.
В нашем случае дифференциальные уравнения тела запишутся:

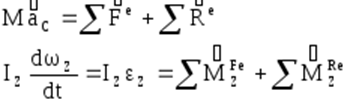
Примечание1. В общем случае при вращении относительно нецентральной оси Z уравнения движения запишутся:

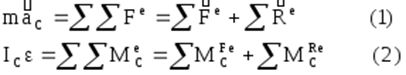
Выше было показано, что уравнение(2) эквивалентно уравнению

I_ze=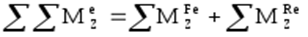 

Выполним переход Даламбера, обозначив:

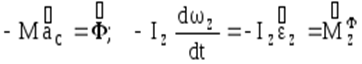
Таким образом: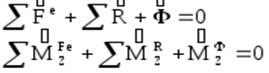

Получили: В любой момент времени:

- геометрическая сумма внешних сил, сил реакции связей и силы инерции, условно приложенной к центру масс вращающегося тела, уравновешивается;

- геометрическая сумма моментов внешних сил, моментов сил реакции связей и момента от силы инерции, условно приложенной к телу, относительно оси вращения, уравновешивается.

При использовании метода кинетостатики для вращательного движения тела векторное уравнение сил целесообразно записывать в естественных осях:

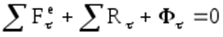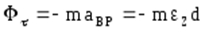
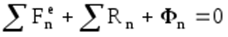 где 

  где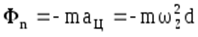 

Поскольку момент от сил инерции относительно оси Z создается только касательной составляющей, то можно указать точку её приложения на линии О d:

Ф_t * ОЦ=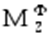  или me _z d ОЦ=I_ze _z
откуда ОЦ=

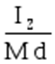
Легко заметить, что при вращении тела относительно оси Z, проходящей через центр тяжести тела(точку С) силы инерции в уравнение кинетостатики не войдут, так как d=0. При равномерном движении тела(e _z=0) в уравнения кинетостатики не войдёт момент от сил инерции.

в) При плоском движении твёрдого тела.

При плоском движении твёрдого тела его дифференциальные уравнения имеют вид:

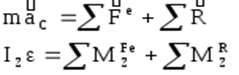
Выполняя переход Даламбера, обозначив 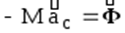 и 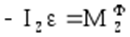 будем иметь: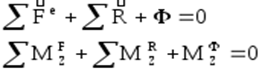 

проекциях на оси координат система (4) запишется:

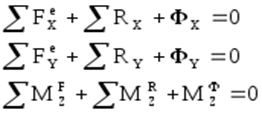
В заключение отметим, что в самом общем случае движения твёрдого тела и вообще механической системы в пространстве, заданном осями XYZ уравнения кинетостатики имеют вид:

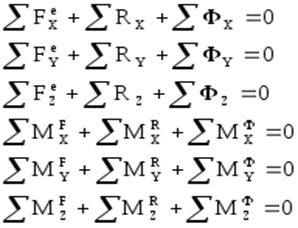
Если в системе уравнений (4) отбросить силы инерции и моменты от сил инерции, то получим обычные уравнения статики для пространственной системы сил. Найденные реакции в этом случае называются статическими реакциями. Если наоборот отбросить действующие силы и их моменты и определить реакции только от инерционных слагаемых, то получим динамические реакции. Решения системы (4) в полном объёме позволяют вычислять полные реакции механической системы.