Работаи мощность

Работа постоянной и переменной сил.

Работа постоянной силы. Работой  постоянной силы называется скалярное произведение вектора силы и вектора перемещения 
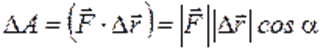:  ; где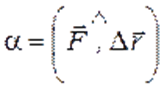 
Работа – скаляр. Если на тело действует несколько сил (N – число сил), и вектор перемещения тела равен , то совершаемая работа равна алгебраической сумме работ, совершаемых каждой из действующих на тело сил на этом перемещение 
Работа переменной силы. Если рассматриваемый участок траектории разбивается на большое число 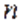 элементарных участков, то длина пути элементарного участка будет близка к величине перемещения на этом участке 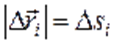 Путь ограничен точками С и D (рисунок)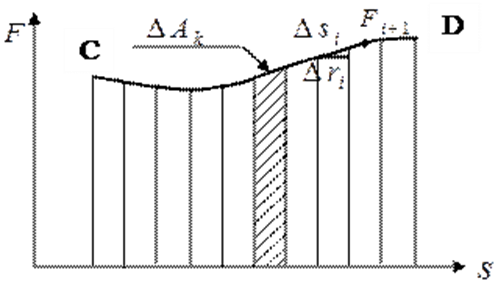

Рисунок 1.2.1. – Зависимость переменной силы от пути   При бесконечно большом количестве участков, на которое разбивается путь ()
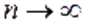приращения величин перейдут в бесконечно малые величины 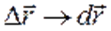,  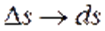а работа переменной силы на участке пути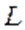 
 выражается криволинейным интегралом: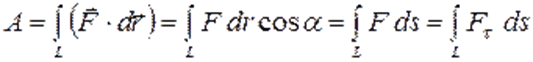
где 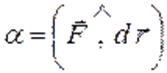 ,  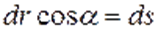Если силу разложить на касательную и нормальную составляющие, то работу составляет только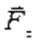 

– касательная составляющая силы, направленная по касательной в каждой точке траектории.

Силы, работа которых по замкнутому контуру равна нулю, называются потенциальными. В механике к потенциальным силам относятся сила тяжести и сила упругости.

Консервативными называются силы, работа которых не зависит от формы траектории, а определяется только положением её начальной и конечной точек.

К классу консервативных относятся, например, гравитационные силы, упругие, силы электростатического взаимодействия.

Кинетическая энергия материальной точки и механической системы и ее связь с работой внешних и внутренних сил, приложенных к системе.

Кинетическая энергиямеханической системы - это энергия механического движения этой системы.

Кинетическую энергию материальной точки массой m, движущейся с абсолютной скоростью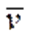  

определяют по формуле: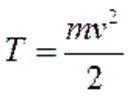 

где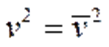 

Кинетическая энергия механической системы равна сумме кинетических энергий всех точек этой системы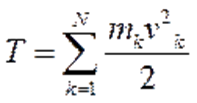 

Работа и мощность при вращательном движении, КПД

Часто встречаются детали машин, вращающиеся вокруг неподвижных осей. Причиной вращательного движения является приложенный к телу вращающий момент относительно оси, который создается парой сил или силой F (рис. 137) и определяется по формуле M = F .D/2.

При повороте тела (рис. 137) на малый угол dφ работа совершается силой F, точка приложения которой перемещается из положения C1 в положение C2. Полное перемещение точки приложения силы равно длине дуги d s = R dφ радиусом R.

Так как сила F все время направлена по касательной к перемещению s, то совершаемая ею работа определится как произведе­ние силы на перемещение

dW = F ds = FR dφ = F D/2 dφ.

Произведение силы на радиус определяет вращающий момент, т. е. F D/2 = M. Учитывая это, окончательно находим dW = M dφ. Интегрируя, получим W = M φ. (164)

Работа вращающего момента равна произведению момента на угол поворота.

Определим мощностьпри вращательном движении

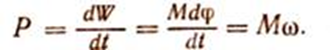
Мощность при вращательном движении тела равна произведению вращающего момента (момента пары) на угловую скорость.

Подставив в выражение мощности значение угловой скорости, выраженной через частоту вращения (об/мин)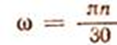  

получим 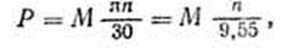 откуда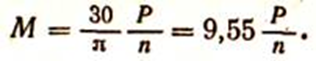 

При данной мощности двигателя максимальный вращающий момент, который двигатель способен развить, можно изменить путем варьирования частоты вращения. Уменьшая частоту вра­щения, увеличивают вращающий момент и, наоборот, увеличивая частоту вращения, вращающий момент уменьшают.

Пример. Определить численные значения силы, приложенной к ободу шкива (рис. 137), если она передает мощность Р = 4 кВт при числе оборотов п = 60 об/мин, диаметр шкива В = 0,5 м.

Решение. На основании уравнения (166) находим вращающий момент Мвр = 9,55 Р/п, кроме того, Мвр = F D/2 Приравнивая значения моментов, находим силу F

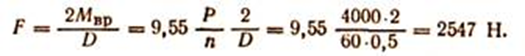
Если алгебраическая сумма проекций на какую либо ось всех действующих сил системы ровна 0, то проекция её вектора количества движения на эту ось есть величена постоянная.

Общие теоремы динамики

При решении многих инженерных задач нет необходимости в подробном описании поведения всей механической системы. Достаточно знать, как меняются лишь некоторые, основные для данной задачи параметры. Законы изменения таких величин представляют собой общие теоремы динамики.

Теорема о движении центра масс

Центр масс механической системы движется так же, как материальная точка с массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему.

m rC = Re илиm aC = ∑Fke .

Из формулировки теоремы следует, что внутренние силы непосред-

ственно не влияют на движение центра масс системы.

Теорема об изменении количества движения

Производная по времени от главного вектора количества движения

механической системы равна векторной сумме всех внешних сил, дейст-

вующих на систему 

После интегрирования последнего выражения по времени в пределах

от 0 до t получим теорему в конечной форме.

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов всех внешних сил, действующих на систему за то же время

Q −QO = ∑Ske .

k

Внутренние силы не входят явно в формулировку теоремы и, поэтому, не могут непосредственно изменять количества движения системы.

Теорема об изменении главного вектора кинетического момента

Первая производная по времени от кинетического момента системы, вычисленного относительно центраO , равна геометрической сумме моментов всех внешних сил, действующих на систему, взятых относительно того же центра

ddt KO = ∑MO (Fke ).

Теорема о кинетическом моменте в относительном движении по отношению к центру масс

Теорема об изменении кинетического момента относительно центра масс в относительном движении сохраняет тот же вид, что и относительно

неподвижного центра в абсолютном движении

Теорема об изменении кинетической энергии

Дифференциал от кинетической энергии системы равен сумме эле-

ментарных работ всех внутренних и внешних сил, действующих на систему d T = ∑δ Ake + ∑δ Aki .

Проинтегрировав это соотношение, получим конечную формулиров-

ку данной теоремы

T −T0 = ∑Ak e + ∑Ak i .

k k

Её можно записать и в форме мощностей внешних и внутренних сил

Отличительной особенностью теоремы об изменении кинетической энергии системы состоит в том, что только в одной этой теореме из всех общих теорем динамики системы внутренние силы явным образом фигурируют в формулировке теоремы.