Прочность при динамических нагрузках

Понятие о динамических нагрузках в деталях и узлах подвижного состава железнодорожного транспорта

Нагрузка, передаваемая подвижным составом на рельсы при движении, называется динамической. Динамическое воздействие подвижного состава на путь определяется сложными колебательными процессами, возникающими при движении. Они обусловлены наличием различных неровностей на поверхностях соприкасания колес с рельсами, упругой деформируемостью пути, рессор и других элементов ходовых частей, особым характером движения жестко соединенных между собой осей подвижного состава в рельсовой колее при изменяющейся по протяжению пути траектории движения подвижного состава.

В общем случае взаимодействие пути и подвижного состава определяется особенностями конструкций ходовых частей подвижного состава и рельсовой колеи, а также качеством технического содержания локомотивов, вагонов и пути.

Каждая единица подвижного состава состоит из неподрессоренной и подрессоренной частей. К неподрессоренной части относят массу колесных пар, букс и примерно 2/3 массы рессор. Все остальное составляет подрессоренную часть. При движении подрессоренные и неподрессоренные части локомотивов и вагонов совершают колебательные движения относительно пути и друг друга и это вызывает изменения нагрузок на рельсы. При движении поезда на рельсы действуют и переменные горизонтальные поперечные силы: рамное давление (силы, действующие на кузов и передаваемые через раму на колесные пары), а также боковое давление, вызванное поворотом состава в кривых (вписывание подвижного состава в кривые). Рельсы воспринимают также и горизонтальные продольные силы (силы угона, торможения и продольные усилия от действия температуры).

При конструировании верхнего строения пути и ходовых частей подвижного состава стремятся достигнуть возможно более благоприятного их взаимодействия.

Рельсовой колеей называются две геометрические линии, проходящие вдоль пути по внутренним граням головок рельсов на уровне их контакта с гребнями колес.

Основным требованием при проектировании и устройстве рельсовой колеи является обеспечение безопасности движения поездов с установленными скоростями при минимуме сил взаимодействия рельсового пути и подвижного состава.

В кривых участках железнодорожного пути рельсовая колея устраивается с учетом следующих особенностей:

1. При движении железнодорожного экипажа по кривой появляется сила инерции, которую обычно называют центробежной силой. Эта сила создает дополнительное давление на наружную рельсовую нить и вызывает крен кузова на рессорах, в связи с этим рельсы быстрее изнашиваются, возникают отбои рельсовых нитей, увеличиваются напряжения в элементах верхнего строения пути, пассажиры испытывают неприятные ощущения. С целью нейтрализации вредного влияния центробежной силы в кривых приподнимают наружную рельсовую нить над внутренней, т. е. устраивают возвышение наружной рельсовой нити.

2. При переходе экипажа из прямой непосредственно в круговую кривую внезапно появляется центробежная сила. Для исключения динамического эффекта – внезапного воздействия экипажа на путь, вызывающего боковой толчок при входе экипажа в кривую и выходе их нее, между круговой кривой и прямой устраивают особую кривую – переходную.

3. Для облегчения вписывания (прохода) тележек экипажей в кривые участки пути (R < 350 м) устраивают уширение рельсовой колеи.

4. Для соблюдения требований габарита приближения строений (С) в кривых двухпутных линий увеличивают междупутные расстояния.

5. С целью обеспечения расположения рельсовых стыков в одном створе (по «наугольнику») укладывают по внутренней нити укороченные рельсы.

Силы инерции при расчете на прочность.

При расчетах на прочность элементов конструкций с учетом сил инерции динамическая задача сводится к статической с помощью принципа…

1)суперпозиции

2)Даламбера

3)начальных размеров

4)Сен-Венана

2Элемент AB постоянного поперечного сечения прикреплен к оси О-О и вращается вокруг нее. Максимальное нормальное напряжение от сил инерции действует в сечении…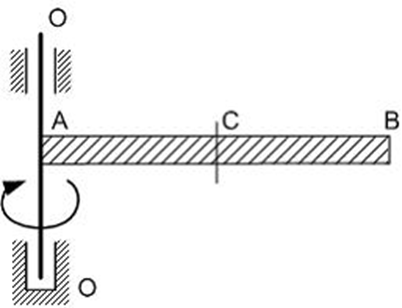

все сечения равноопасны

A

C

B

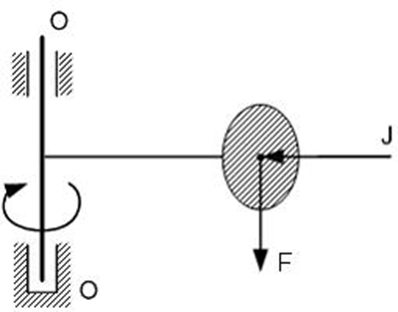
3Груз весом F равномерно вращается вокруг оси O – O, к которой он прикреплен стержнем. Правильная расчетная силовая схема показана на рисунке…

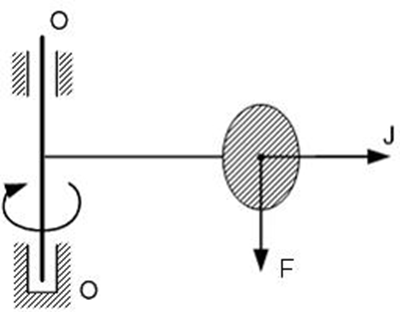
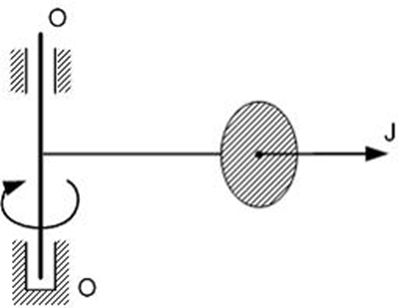
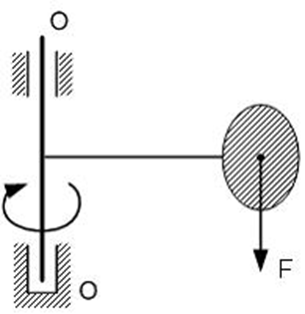
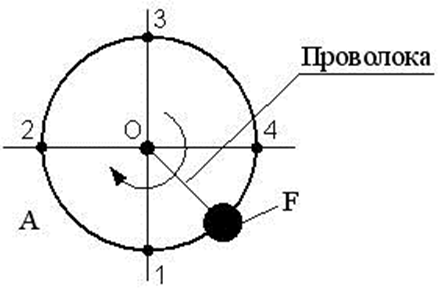
4Тело весом F равномерно вращается в вертикальной плоскости вокруг оси, проходящей через точку O. Напряжения в проволоке будут максимальными, когда тело находится в положении…

5 Груз весом F подвешен на тросе и поднимается с постоянным ускорением а . При определении напряжений в тросе (без учета массы троса) необходимо дополнительно учитывать инерционную нагрузку, равную…

1) 

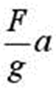
2)

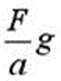
3)

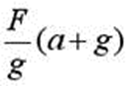
4)

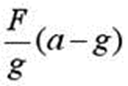
6 Груз весом F подвешен на тросе с площадью сечения A и поднимается с постоянным ускорением a . Условие прочности по напряжениям для троса (без учета веса троса) имеет вид…

1)

2)

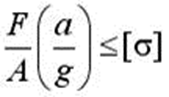
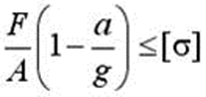
3)

4)
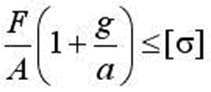
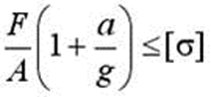
7 Стержень длиной L с площадью поперечного сечения A имеет на конце груз массой m и вращается вокруг оси О-О с постоянной угловой скоростью w . Условие прочности стержня по напряжениям (без учета веса груза и массы самого стержня) имеет вид…



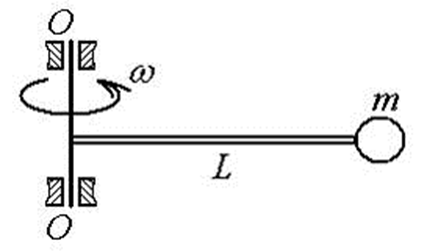
1)
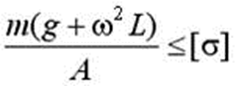
2)
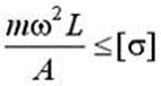
3)
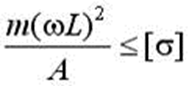
4)
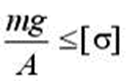
Кольцо с площадью поперечного сечения A равномерно вращается с постоянной угловой скоростью w . Обозначим 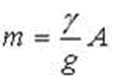 массу единицы длины кольца ( y –вес единицы объема материала). Условие прочности по напряжениям имеет вид…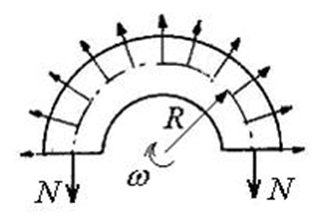


1)
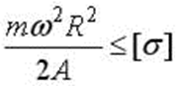
2)
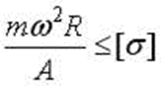
3)
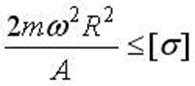
4)

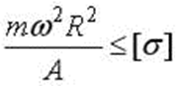
Динамическое напряжение, динамический коэффициент.

Напряжения, возникающие при колебаниях деталей, могут во мно­го раз превосходить по своей величине напряжения от действия ста­тических нагрузок.

Расчет деталей сооружений на динамическую нагрузку более сло­жен, чем расчет на статическую нагрузку. Трудность заключается, с одной стороны, в более сложных методах определения внутренних усилий и напряжений, возникающих от действия динамической на­грузки, и, с другой — в более сложных методах определения меха­нических свойств материалов при динамической нагрузке.

Например, при действии ударной нагрузки (т. е. нагрузки чрез­вычайно малой продолжительности) многие материалы, которые при статическом действии нагрузок оказывались пластичными, работают как хрупкие; при действии многократно повторяющейся переменной нагрузки прочность материалов резко снижается.

Общий метод расчета на динамическую нагрузку основан на известном из теоретической механики принципе Даламбера. Согласно этому принципу, всякое движущееся тело может рассматриваться как находящееся в состоянии мгновенного равновесия, если к действующим на него внешним силам добавить силу инерции, равную произведению массы тела на его ускорение и направленную в сторону, противоположную ускорению. Поэтому в тех случаях, когда известны силы инерции, без всяких ограничений можно применять метод се-чений и для определения внутренних усилий использовать уравнения равновесия. В тех же случаях, когда определение сил инерции затруднительно, так, например, при ударе, для определения динамических напряжений и деформаций используется закон сохранения энергии.

10.1.1 Вычисление напряжений при равноускоренном движении

Во многих случаях ускорения, с которыми перемещаются детали машин, известны. Динамические напряжения в этих случаях вычис­ляются без затруднений.

Рассмотрим случай подъема груза весом G вверх с ускорением а (рис. 10.1). Оп­ределить напряжение в канате, пренебрегая его весом.

Прикладываем к грузу силу инерции, равную та = Gа/g и направленную вниз. Применим метод сечений. Делаем разрез n-п иотбрасы­ваем верхнюю часть каната. Усилие в канате обозначаем N_д. Так как напряжения при центральном растяжении равномерно распределены по сечению, то можем принять, что

N_д = s_д × А,

где s_д - искомое динамическое напряжение.

Проектируя все силы, в том числе и силы инерции, на вертикальную ось, получаем

,

откуда

где - напряжение при статическом действии груза;

- динамический коэффициент.

Таким образом, динамические напряжения могут быть выражены через статические напряжения и динамический коэффициент. Это особенно удобно, так как величину динамического коэффициента часто приходится определять опытным путем.

Рассмотрим случай продольного удара груза по неподвиж­ному телу. Пусть груз весом G падает с высоты h на неподвижный стержень

Скорость тела в момент удара определяется по известной формуле свободного падения

Эта скорость за очень короткий промежуток времени удара, исчисляемый тысячными или сотыми долями секунды, упадет до нуля.

Благодаря большой величине ус­корения (замедления) возникает значительная сила инерции, вели­чиной которой и определяется действие удара.

Однако теоретически трудно установить закон изменения скорости, а, следовательно, и величину силы инерции. Здесь применяется другой путь, основанный на законе сохранения энергии и на следующих до­пущениях:

1. Напряжения при ударе не превосходят предела пропорциональности, так что закон Гука при ударе сохраняет свою силу.

2. Тела после удара не отделяются друг от друга.

3. Масса неподвижного стержня считается малой по сравнению с массой ударяющего тела, поэтому в расчет не принимается.

4. Потерей части энергии, перешедшей в теплоту и в энергию коле­батель-ного движения соударяющихся тел, пренебрегаем.

Приравняем работу падающего груза потенциальной энергии де­формации стержня.

Работа, совершаемая весом падающего груза, где - перемещение в точке удара, равное укорочению стержня.