Изгиб, основные понятия и определения.

Изгиб представляет собой такую деформацию, при которой происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев (рис. 16.1). Изгиб связан с возникновением в поперечных сечениях бруса изгибающихся моментов. Изгибающий момент — внутренний силовой фактор (внутреннее усилие), возникающий в поперечном сечении бруса; он действует в плоскости, перпендикулярной к поперечному сечению бруса. Различают частные случаи изгиба: поперечный, прямой, чистый, косой, продольный, продольно-поперечный; более подробно о наиболее простых видах изгиба изложено ниже.

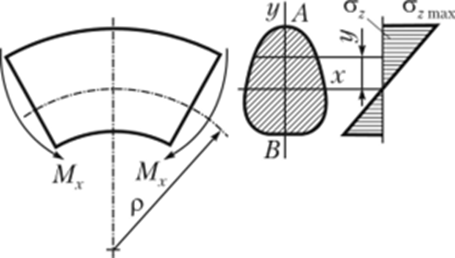
Рис. 16.1. Изгиб бруса произвольного сечения

В частности, прямой изгиб возникает, когда на прямой брус действует нагрузка в виде системы сосредоточенных сил, расположенных в одной плоскости, проходящей через одну из главных центральных осей инерции каждого поперечного сечения бруса.

В случае чистого изгиба в поперечном сечении бруса действуют только нормальные напряжения (см. рис. 16.1)

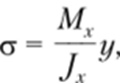
где М_у — изгибающий момент относительно оси х; у — расстояние от нейтральной линии до точек, в которых определяется напряжение ст₂; J_x — осевой момент инерции поперечного сечения относительно главной центральной оси х.

Нейтральная линия — это геометрическое место точек, в которых нормальное напряжение а. в поперечном сечении равно нулю. При простом изгибе нейтральная линия совпадает с главной центральной осью поперечного сечения. На рис. 16.1 приведена эпюра нормальных напряжений при чистом простом изгибе, экстремальных значений эти напряжения достигают в точках Aw В.

Наибольшее по абсолютной величине напряжение ст_гтах находится в точке, наиболее удаленной от нейтральной линии (на расстоянии г/_шах)

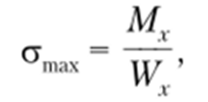
где  

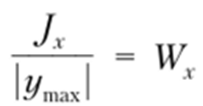
осевой момент сопротивления, или момент сопротивления при изгибе, геометрические характеристики J_x, W_x и др. приведены ниже.

Классификация видов изгиба.

Изгиб — вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев.

Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент.

Прямой изгиб возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения.

Косой изгиб в случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения.

Поперечный изгиб – это такой вид нагружения, при котором в поперечных сечениях бруса возникают не только изгибающие моменты Мх, но и поперечные силы Qу

Чистый косой – два изгибающих момента.

Поперечный косой – два момента и две силы.

Чистый прямой – один момент.

Поперечный прямой – один момент и одна сила.

Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб.

Внутренние силовые факторы:

Изгибающий момент, численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения.

Поперечная сила, численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки.

Эпюры поперечных сил и изгибающих моментов

Эпюрами внутренних поперечных сил и изгибающих моментов называют графическое представление распределения функций Q и M по длине балки при изгибе.

Посмотреть подробные примеры построения эпюр >>

Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.

Рассмотрим некоторые примеры на построение эпюр в балках:

Эпюры при чистом изгибе

Для консольной балки: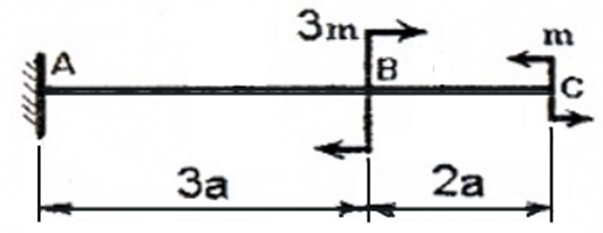

Рис. 1

имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.

Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z₁ ≥ 2a (рис. 2 а,г)

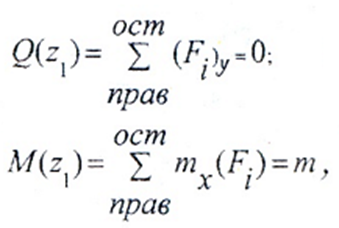
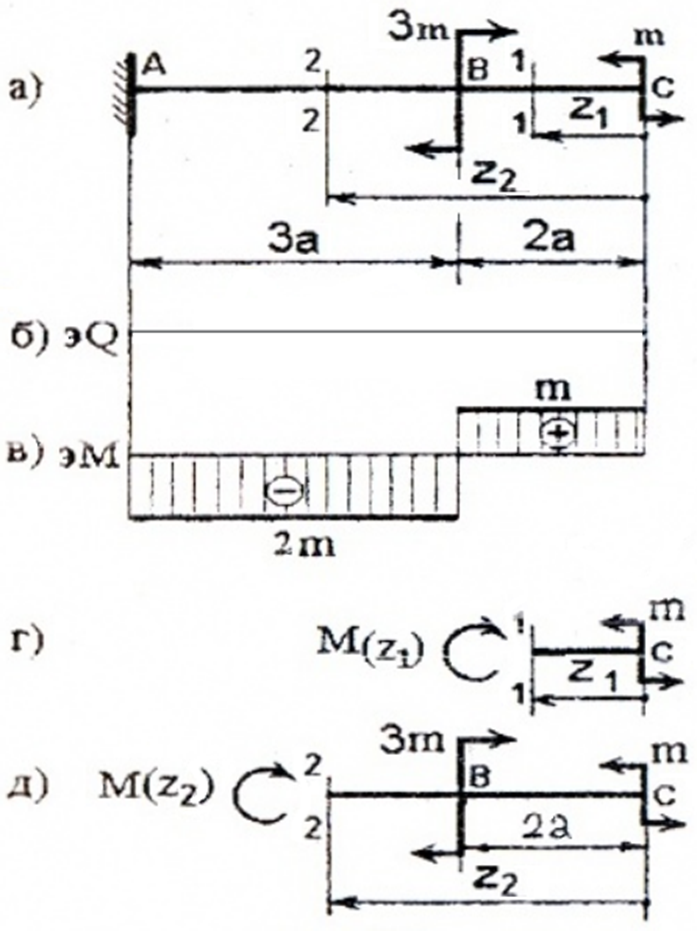
Рис. 2

т.е. Q(z₁)=0 на всем участке, а M(z₁)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.

II силовой участок (AB): 2a ≥ z₂ ≥ 5a (рис. 2 а,д)

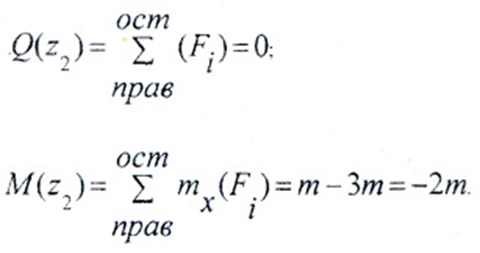
Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).

Более нагруженным оказался участок AB, он и является опасным: M_max=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.

Нормальные напряжения при изгибе.

 Нормальные напряжения при изгибе

Подставляя зависимость (6.6) в формулу (6.5), получаем выраже-

ние для нормальных напряжений в произвольной точке поперечного сечения

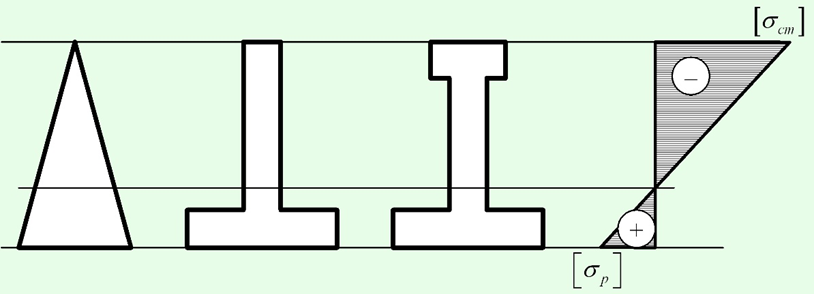
Условно эпюра σ (y) изображается в плоскости сечения (рис. 6.6,б,в). Знаки напряжений на эпюре ставятся в зависимости от направления изгибающего момента M в сечении (на рис. 6.6,б знаки показаны для момента отрицательного направления). Если сечение несимметричное относительно нейтральной линии, то максимальные растягивающие и сжимающие нормальные напряжения будут различной величины (см. рис. 6.6,в).

Момент сопротивления Wx для сечений различной формы определяется через момент инерции Jx сечений (см. раздел “Геометрические характеристики сечений”). Например, для типовых сечений получим:

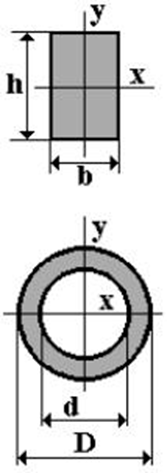
прямоугольное сечение со сторонами b и h:

Рациональные поперечные сечения балок.

Рациональные формы сечения балок

Рациональными формами сечения балок являются такие сечения, которые имеют высокие геометрические характеристики (момент инерции IxIx – с точки зрения максимальной жесткости и момент сопротивления WxWx – с точки зрения максимальной прочности) при одинаковой площади сечения AA. При этом необходимо учесть, что высота сечения ограничена.

Идеальным случаем компоновки сечения является размещение по всей площади верхней и нижней гранях, то есть в местах с максимальными напряжениями.

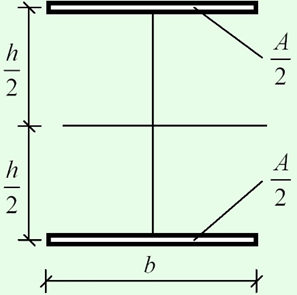
Момент инерции этого сечения

Ix=2⋅A2⋅(h2)2=Ah24Ix=2⋅A2⋅(h2)2=Ah24

Момент сопротивления

Wx=Ixh/2=0,5AhWx=Ixh/2=0,5Ah– теоретически максимально возможное значение момента сопротивления сечения.

В реальных сечений значениеWxWxбудет меньше и по нему можно судить о рациональности того или иного сечения.

Для прямоугольникаWx=bh26=bh⋅h6=0,167AhWx=bh26=bh⋅h6=0,167Ah.

Для кругаWx=πd332=18πd24⋅d=0,125AhWx=πd332=18πd24⋅d=0,125Ah.

Для трубчатого сечения при отношении диаметровα=dD=0,9α=dD=0,9Wx=0,226AhWx=0,226Ah.

Для прокатных профилей

– двутаврыWx=0,31..0,34AhWx=0,31..0,34Ah

– швеллерыWx=0,3..0,33AhWx=0,3..0,33Ah

– неравнобокие уголкиWx=0,14..0,15AhWx=0,14..0,15Ah

– равнобокиеWx=0,12..0,13AhWx=0,12..0,13Ah

Все предыдущие выводы относятся к материалам, которые имеют одинаковые допустимые напряжения на растяжение и сжатие.

Для материалов, для которых допустимые напряжения на растяжение значительно меньше допустимых напряжений на сжатие (такие материалы как чугун) целесообразно распределение материала в сечении сделать так, чтобы максимальные напряжения в сжатой и в растянутой зоне были равны допустимым. Для этого необходимо увеличить площадь сечения растянутой зоны, то есть рациональным будет несимметричный сечение.

Линейные перемещения

Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.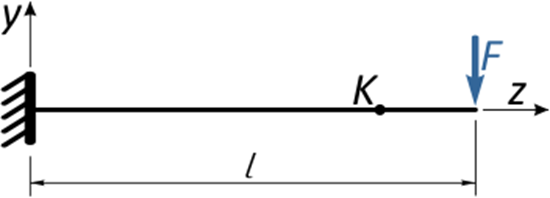



Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.

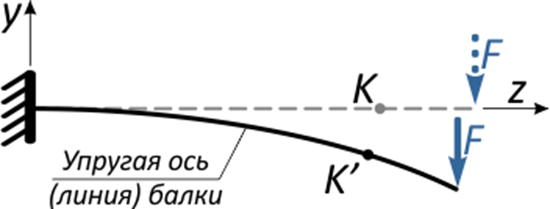
Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (y_K)
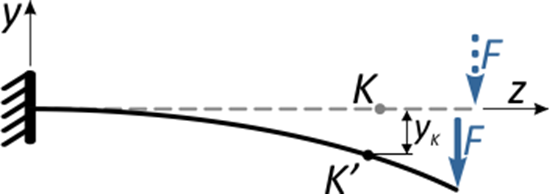
и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — z_K


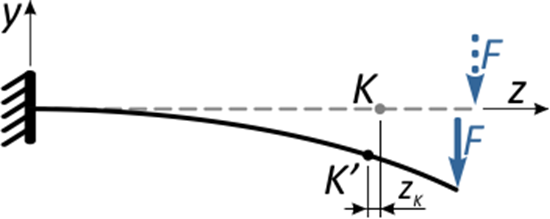
Практические расчеты показывают, что осевые смещения как правило, 

несоизмеримо меньше вертикальных перемещений (например, в данном случае z_K<< y_K), поэтому ими пренебрегают, ограничиваясь вычислением прогибов.

Линейные перемещения (прогибы балки) измеряются в метрах или кратных единицах измерения (миллиметрах и сантиметрах).

Прогибы, при которых сечение в результате деформации балки перемещается вверх принимаются положительными.

Именно по величине прогибов определяется жесткость балки.

Угловые перемещения

Кроме линейных, сечения балки при изгибе получают и угловые перемещения.
Проведем касательные к продольной оси балки в точках K и K’.



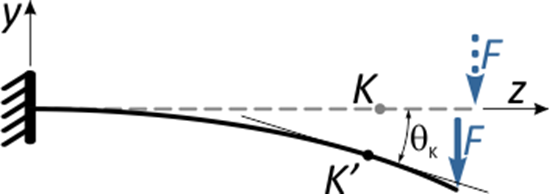
В первом случае линия касательной совпадает с прямой осью балки, во втором – располагается под углом θ.
Угол между касательными очевидно равен углу между нормалями к оси балки в этих точках.

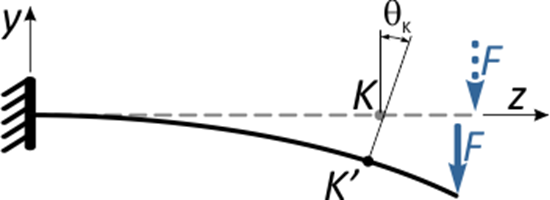
Этот угол θ_K называется углом наклона сечения K в результате деформации балки.

Вычисляется в радианах, с последующим переводом в градусы.

Между линейными и угловыми перемещениями при изгибе существует дифференциальная зависимость.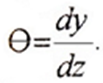

Например, в сечениях, углы наклона которых равны нулю следует ожидать экстремума изогнутой линии балки на данном участке.

Расчёт на жёсткость.

Диаграмма растяжения содержит сведения о механических свойствах материала. Зная предел пропорциональности, предел текучести и предел прочности, можно установить для каждой инженерной задачи величину напряжения, которое можно рассматривать как безопасное напряжение. Это напряжение называют допускаемым или предельным напряжением.

Расчет на прочность ведется по первой группе предельных состояний по наибольшим, т. е. расчетным нагрузкам.

Предельное состояние строительного объекта18 – состояние строительного объекта, при превышении характеристик которого его эксплуатация недопустима, затруднена или нецелесообразна.

наибольшее по абсолютному значению напряжение в опас-

ном сечении, Па; Nрасч − продольная сила в опасном сечении от расчетных нагрузок, Н; A − площадь опасного сечения с учетом ослаб-

лений, м2; R − расчетное сопротивление материала бруса, Па. Расчетное сопротивление материала R получают путем деления

нормативного сопротивления Rn на коэффициент надежности по ма-

териалу. Для металла γm = 1,025–1,15, бетона γm = 1,3–1,5 (табл. 11.2):

R = Rn .

γm

18 Надёжность строительных конструкций и оснований. Основные положения: СТО 36554501- 014-2008: введ. в действие 23.09.2008. М.: ФГУП «НИЦ Строительство», 2008. 16 с.

244