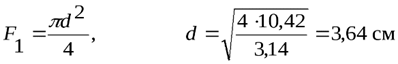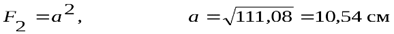Растяжение и сжатие
Характеристика деформации.
Под действием внешних сил твердые тела изменяют свою форму: удлиняются, изгибаются и т.д.
а) растяжение (сжатие)
|
|
Силы Длина стержня ℓ получит положительное (при растяжении), либо отрицательное (при сжатии) приращение Dℓ, т.е. в общем случае длина определяется формулой: L= ℓ ±Dℓ |
Величина, численно равная отношению приращения размера тела, к начальному размеру, называется относительной деформацией.
Относительная деформация сжатия (-) и растяжения (+)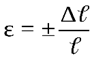 (1)
(1)где ε– величина безразмерная.
Из закона сохранения массы следует, что при растяжении или сжатии должна меняться не только длина тела, но и его поперечный размер. Изменение поперечных размеров тела при его растяжении или сжатии характеризуется относительным поперечным растяжением или сжатием.
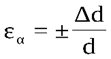
Отношения относительной поперечной деформации εα к его относительной продольной деформации ε называетсякоэффициентом Пуассона
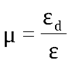
μ – величина табличная. Для металлов μ ~ 0,25, для материалов типа резины μ ~ 0,5.
μ< 0,5 – всегда.
|
б) сдвиг
|
Деформация сдвига может быть представлена в виде деформаций растяжения вдоль диагонали АВ и сжатия вдоль диагонали СД. При деформации сдвига любая прямая, первоначально перпендикулярная к горизонтальным слоям, повернется на угол φ. Тогда:
γ – относительный сдвиг. |
|
в) кручение
|
Верхнее сечение закреплено, к нижнему приложена пара сил и нижнее основание поворачивается по отношению к верхнему на угол φ. Отношение угла закручивания φ к длине стержня Lназываетсяотносительной деформацией кручения.
|
Эпюры продольных сил
Эпюра продольных сил N — это график, показывающий, как изменяется продольная сила по длине бруса.
Пример 1. Построить эпюру продольных сил для бруса, нагруженного осевыми силами (рис. 2.2.5).
Для построения эпюры продольных сил проводим прямую, параллельную продольной оси бруса (базовая линия). Значение нормальных сил откладывают в выбранном масштабе и с учетом знаков (положительные силы откладываем вправо от базовой линии, а отрицательные — влево) на уровне соответствующего участка. Участком считается расстояние от силы до силы, т.е. границами участков являются сечения, в которых приложены внешние силы. В нашем примере у бруса три участка: АВ, ВС и CD.
Штриховка эпюр означает величину продольной силы в любом сечении бруса, проводится перпендикулярно продольной оси стержня.
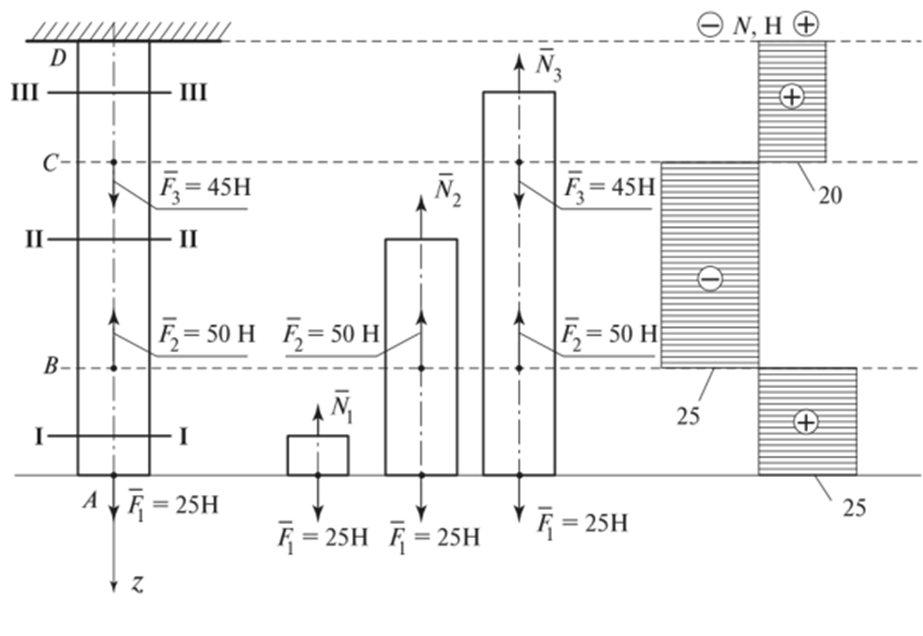
ЭПЮРЫ ПРОДОЛЬНЫХ СИЛ N И НОРМАЛЬНЫХ НАПРЯЖЕНИЙ σ
Эпюра продольных сил N — это график, показывающий, как изменяется продольная сила по длине бруса.
Пример 1. Построить эпюру продольных сил для бруса, нагруженного осевыми силами (рис. 2.2.5).
Для построения эпюры продольных сил проводим прямую, параллельную продольной оси бруса (базовая линия). Значение нормальных сил откладывают в выбранном масштабе и с учетом знаков (положительные силы откладываем вправо от базовой линии, а отрицательные — влево) на уровне соответствующего участка. Участком считается расстояние от силы до силы, т.е. границами участков являются сечения, в которых приложены внешние силы. В нашем примере у бруса три участка: АВ, ВС и CD.
Штриховка эпюр означает величину продольной силы в любом сечении бруса, проводится перпендикулярно продольной оси стержня.
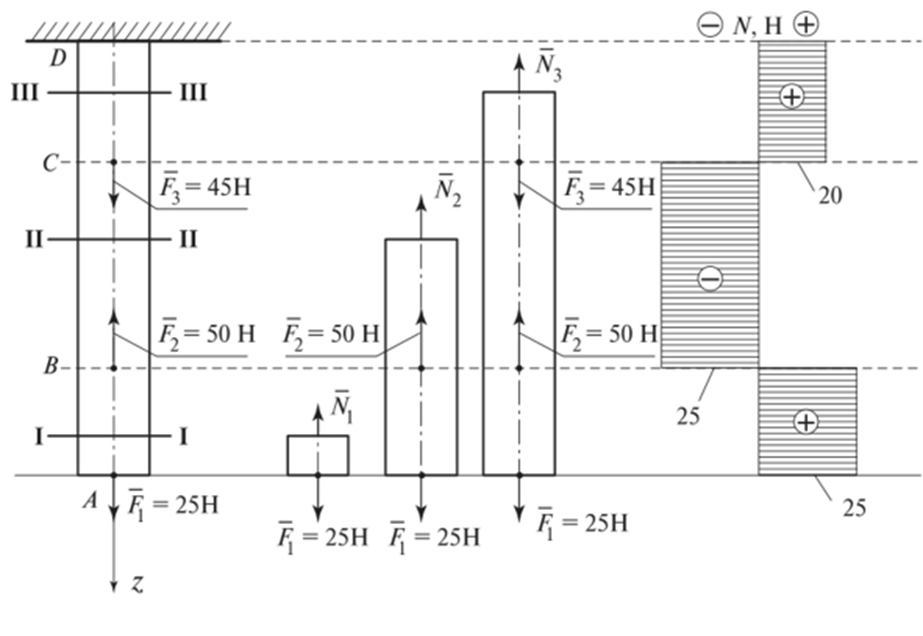
Рис. 2.2.5
Построение эпюр начинаем от свободного конца.
Применяя метод сечений, мысленно рассекаем брус на участке АВ (сечение I—I) и отбрасываем его верхнюю часть. Рассмотрим равновесие оставшейся нижней части: 'ZFz = F] — У, = 0;
Nx = Fv Поскольку Fx направлена от сечения, то N{ = Fx = 25 Н. На всем участке АВ продольная сила положительна (так как участок растягивается). Откладываем ее в масштабе вправо от базовой линии. Далее проводим сечение II—II на участке ВС, мысленно отбрасываем верхнюю часть бруса и рассматриваем равновесие нижней части:
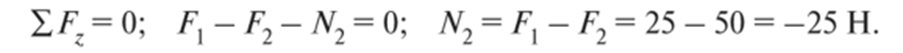
Продольная сила N2 отрицательная и направлена к сечению. Аналогично определяем значение продольной силы в сечении III—III на участке CD:
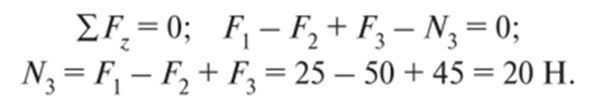
Продольная сила N3 направлена от сечения, т.е. является растягивающей. Итак, продольная сила А в любом сечении равна алгебраической сумме продольных сил, действующих по одну сторону от сечения.
Пример 2. Для бруса со ступенчато-переменным сечением построить эпюрыпродольных сил и нормальных напряжений (рис. 2.2.6).
Эпюра нормальных напряжений а — это график, показывающий, как изменяется напряжение по длине стержня. Правило знаков такое же, как у продольной силы: напряжение положительное — растяжение, напряжение отрицательное — сжатие.
Вопрос об определении нормальных напряжений связан с расчетом бруса на прочность.
При построении эпюры продольных сил участка считается расстояние от силы до силы (в нашем примере четыре участка: АВ, BD, DK, KL).
гг „ (
При построении эпюры нормальных напряжении I с = — I
участком является либо расстояние между силами, либо расстояние между силами и тем местом, где изменяется площадь поперечного сечения (в нашем примере шесть участков: АВ, ВС, CD, DE, ЕК, KL).
Для построения эпюры продольных сил мысленно рассекаем участок АВ по сечению I—I. Верхнюю часть отбрасываем и рассматриваем равновесие нижней части:
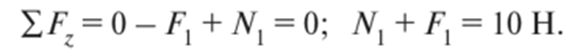
F{ и Nx направлены к сечению, т.е. участок АВ сжимается.
На участке ВС в сечении II—II продольная сила N2 равна алгебраической сумме внешних продольных сил, лежащих ниже этого сечения, N2 = — F{ + F2 = —10 + 15 = 5 Н. На участке CD для эпюры продольных сил никаких изменений не произошло: алгебраическая сумма сил осталась та же: N3 = N2 = 5 Н.
Рассекаем участок DE. Продольная сила N4 равна алгебраической сумме сил —Fx + F2 — F3 = —10 + 15 — 30 = -25 Н. На участке ЕК продольная сила N будет такая же, как на участке DE, т.е. существует только перепад сечения, а сила не приложена, N5 = N4 = — 5 Н.
На участке KL в сечении VI—VI продольная сила 7^ = —10+15 — - 30 + 45 = 20 Н.
Все значения продольных сил Nоткладываем на эпюре.
Скачок на эпюре N находится в том сечении, где приложена сосредоточенная сила, и происходит на величину и в направлении этой силы. Так, в сечении, где приложена сила F{, — скачок от нуля на 10 Н в отрицательную сторону. В том сечении, где действует сила Е2 — скачок в положительную сторону на 15 Н, в результате получим N2 = 5 Н. В сечении, где приложена сила Fv — скачок в отрицательную сторону на величину силы Е3 = —30 Н, в результате на участках DE и ЕК имеем N = —25 Н. Последний скачок в сечении, где действует сила Е4, в положительную сторону на 45 Н, и jV6 = 20 Н. При построении эпюры нормальных напряжений надо учитывать, на какой площади поперечного сечения действует данная продольная сила.
Тогда:

По полученным данным строим эпюру нормальных напряжений а.
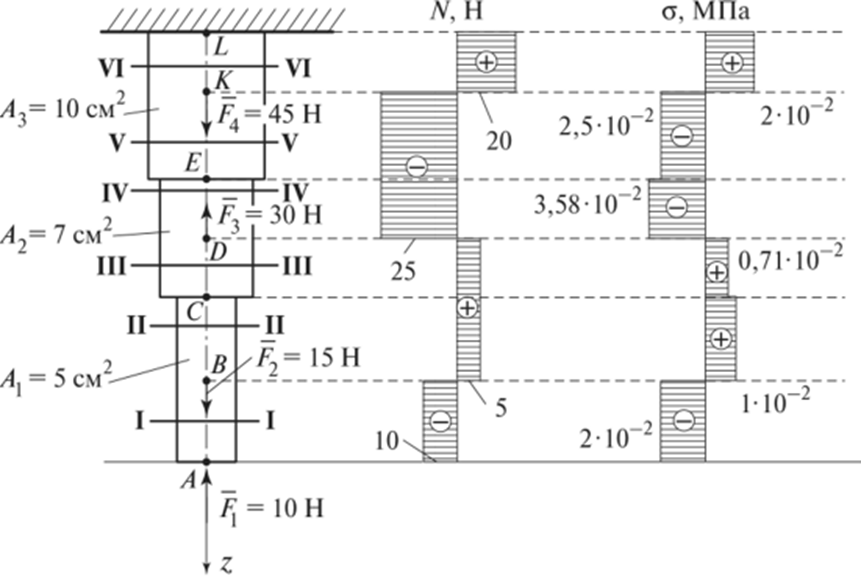
Пример 3. Стержень стоит на плоскости (рис. 2.2.7). Построить для данного стержня эпюры продольных сил N и нормальных напряжений а.
Эпюры нормальных напряжений.
Переходим к эпюре нормальных напряжений. В отличие от продольных сил, нормальные напряжения зависят от формы бурса, а если точнее, то от площади его поперечных сечений и вычисляются они, по следующей формуле:
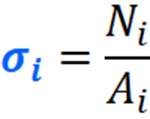
чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на его площадь.
Для того, чтобы построить эпюру нормальных напряжений, нужно рассчитать ее для любого сечения, каждого участка. В отличие, от продольной силы, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашего подопытного бруса, нужно наметить три участка и вычислить напряжение, соответственно, 3 раза:
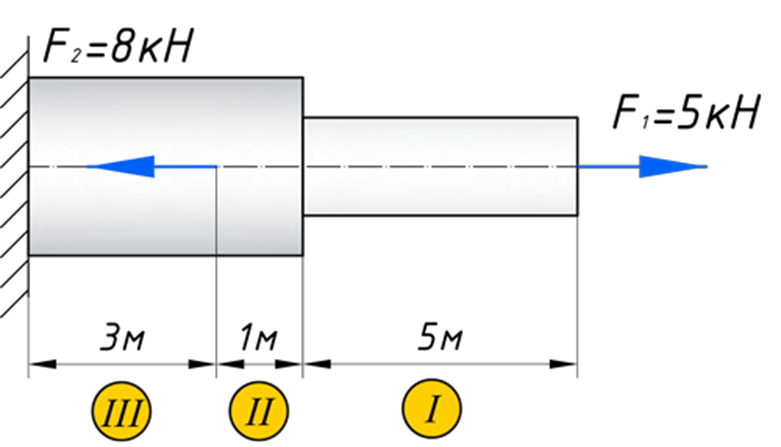
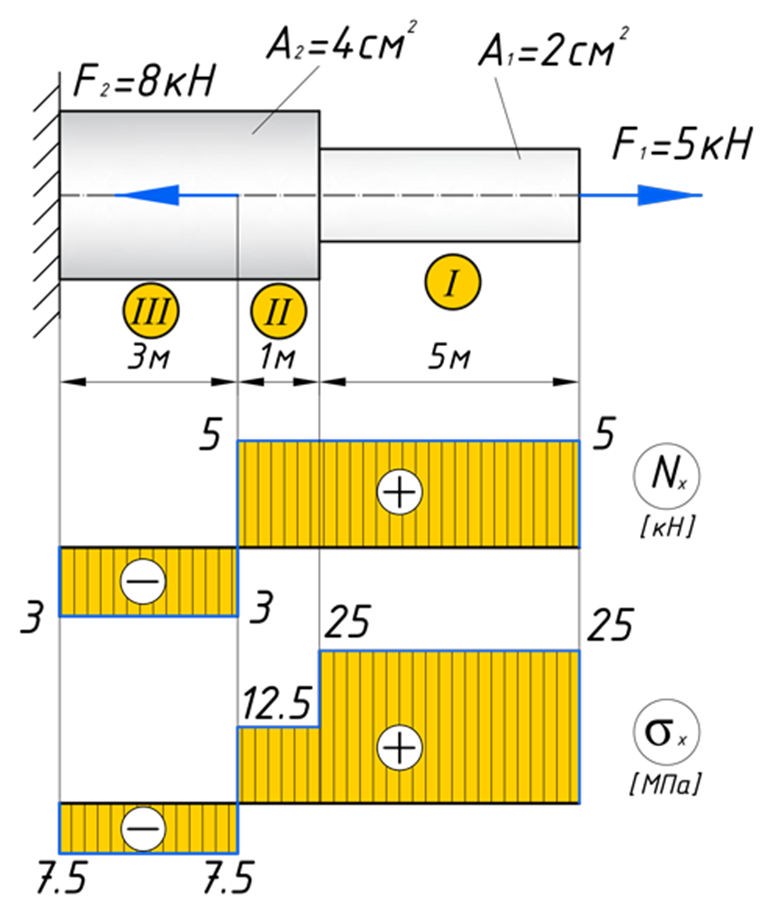
Зададим брусу на первом участке (I) площадь поперечного сечения A1=2 см2, а вторая ступень бруса, допустим, будет иметь площадь A2=4 см2 (II, III участки). В вашей домашней задаче, эти величины будут даны по условию.
Вычисляем напряжения на каждом участке:
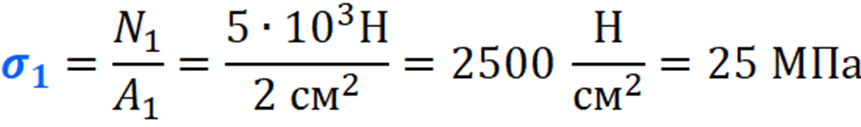
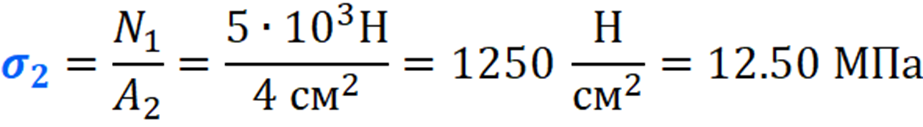
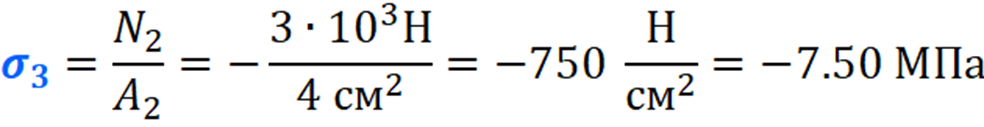
По полученным значениям строим эпюру нормальных напряжений:
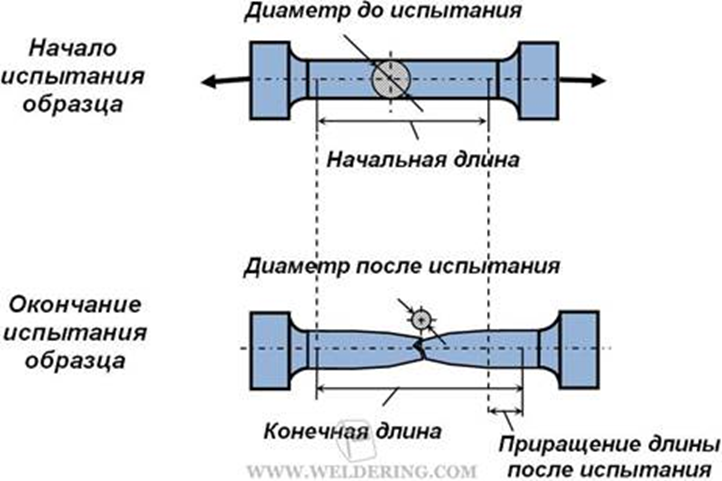
Испытания материалов на растяжение и сжатие при статическом нагружении.
1. Для создания современной конструкции необходимо рассчитать все её детали и узлы на прочность, жесткость, устойчивость. В расчетные формулы входят величины, зависящие от физико-механических характеристик материала деталей. Без знания механических свойств материалов невозможно сделать обоснованный выбор материалов рассчитываемой конструкции при определении ее размеров. Для определения этих характеристик проводятся испытания материалов в строгом соответствии с государственными стандартами. Стандарты [1 ¸ 5] определяют правила подготовки образцов, их форму и размеры, а стандарты [6 ¸24] – методики проведения испытаний.
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
Наиболее чувствительными и точными являются машины с рычажно-маятниковыми силоизмерениями. Они отличаются надежностью силоизмерения и простотой конструкции.
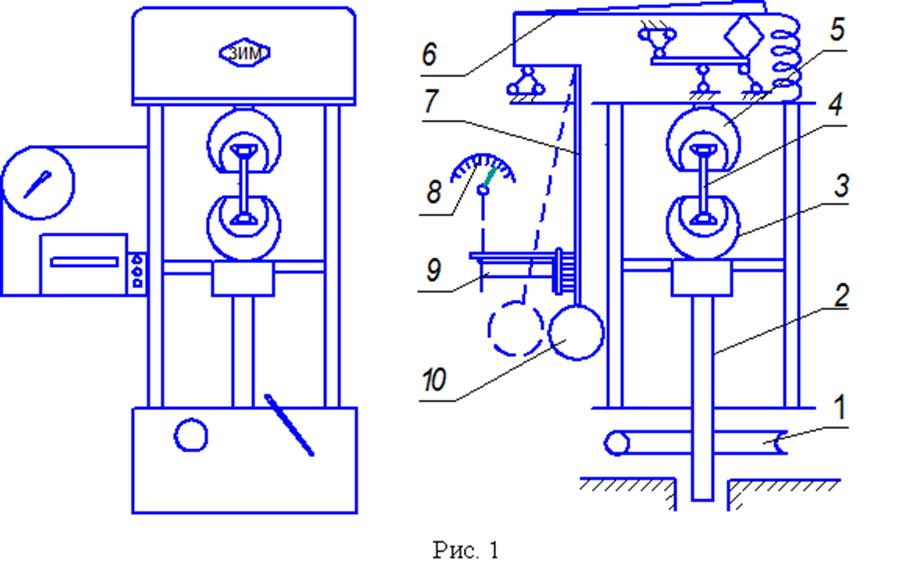
Универсальная испытательная машина УММ-5 с максимальным усилием нагружения 49 кН снабжена рычажно-маятниковым силоизмерителем. Внешний вид испытательной машины УММ-5 и кинематическая схема ее силоизмерительного устройства показаны на рис.1. Машина имеет пять скоростей нагружения, м/с: 3,33-10-5; 6,67-10-5; 1,67-10-4; 3,33-10-4; 8,33-10-4 и одну скорость холостого хода, равную 1,67-10-3 м/с. Максимальное расстояние между захватами равно 0,8 м. Погрешность измерений равна ± 1% от величины измеряемой нагрузки.
Для создания усилия растяжения вращение от электродвигателя передается через червячную передачу 1 на впрессованную в червячное колесо гайку, в которую вворачивается винт 2, связанный с нижним захватом 3. Это усилие через образец 4, верхний захват 5 и систему рычагов 6 уравновешивается весом груза 10, расположенного на конце маятника 7. Маятник связан зубчатой реечной передачей со шкалой нагрузки 8, а также с диаграммным устройством 9. Это устройство через систему зубчатых передач и зубчатую реечную передачу также связано с нижним захватом 3, что позволяет автоматически записывать диаграмму растяжения – график зависимости абсолютного удлинения ∆ℓ от усилия растяжения F.
2) Диаграммы растяжения : машинная диаграмма растяжений и условная диаграмма растяжений
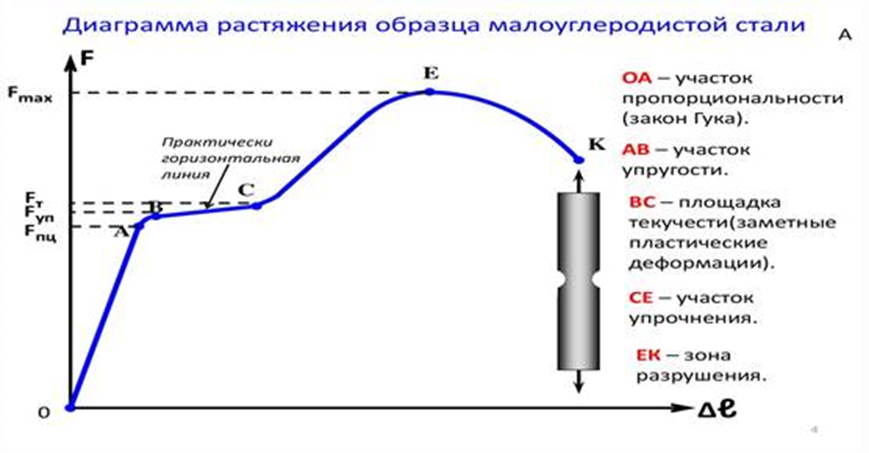
Точка А (1) соответствует пределу пропорциональности: после нее прямая линия ( прямая пропорциональность) заканчивается и переходит в кривую, т.е. участок диаграммы ОА –удлинение растет пропорционально нагрузке, подтверждается закон Гука
Точка В (2) соответствует пределу упругости материала: материал теряет упругие свойства-способность вернуться к исходным размерам
Точка С (3) является концом участка,на котором образец сильно деформируется без увеличения нагрузки.Это явление называют текучестью, т.е. текучесть – удлинение при постоянной нагрузке
Точка Е (4) соответствует максимальной нагрузке, в этот момент на образце образуется « шейка»-резкое уменьшение площади поперечного сечения. Напряжения в этой точке называют временным сопротивлением разрыву или условным пределом прочности. Участок СЕ-участок упрочнения
Точка К (5)- наступает разрушение образца .
Первая диаграмма связана не только со свойствами материала , но и с размерами испытуемого образца. Чтобы получить характеристики свойств материала, исключают влияние на диаграмму размеров образца, для этого диаграмму перестраивают: делят нагрузки F на начальную площадь А0 поперечного сечения образца, а абсолютные удлинения Δ l на начальную длину l0. Диаграмму, построенную в координатах σ-ε, называют диаграммой растяжения материала или условной диаграммой напряжений. По данной диаграмме определяются механические характеристики материала. Отличаются диаграммы масштабом.
3).Основные характеристики прочности (механические характеристики):
Механические характеристики-это числовые характеристики позволяющие оценивать свойства
σпц-предел пропорциональности, наибольшее напряжение, до которого выполняется закон Гука
σпц=F1/А0
σу- предел упругости, наибольшее напряжение , до которого в материале не возникают остаточные деформации
σу= F2/А0
σт-предел текучести, наименьшее напряжение при котором деформация увеличивается без заметного увеличения нагрузки
σт= F3/А0
σв- предел прочности или временное сопртивление, напряжение, соответствующее
максимальной нагрузке, предшествующей разрушению образца
σв= Fмах/А0
4.Виды диаграмм растяжения
Различные материалы по-разному ведут себя под нагрузкой, характер деформаций и разрушения зависит от свойств материала.
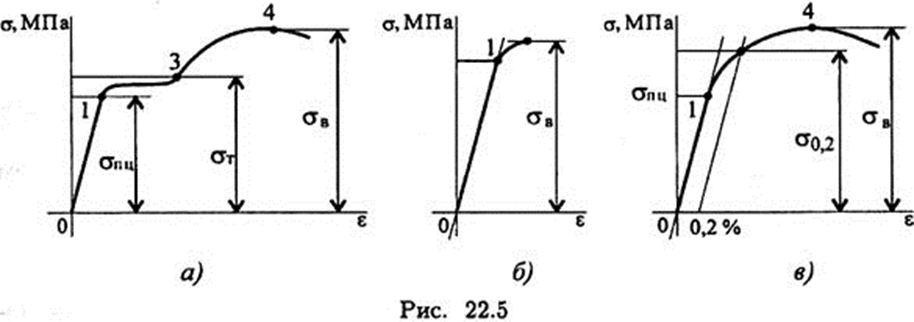
По типу диаграмм растяжения материалы делят на три группы:
1. Пластичные материалы имеют площадку текучести на диаграмме
2. Хрупкие материалы, мало деформируются, разрушаются по хрупкому типу, на диаграмме нет площадки текучести
3. Пластично-хрупкие, не имеющие площадки текучести, но значительно деформирующиеся под нагрузкой. Их деформацию обычно ограничивают. Максимально возможная относительная деформация ε=0,2%. По величине максимально возможной деформации определяется соответствующее нормальное напряжение σ0,2, которое принимают за предельное
5) При проектировании элементов конструкций выбирают материал и определяют размеры элемента, надежно обеспечивающие его прочность.
Напряжения, при которых нарушается прочность элемента, называют предельными. Нарушением прочности считают не только разрушение элемента конструкции, но и появление хотя бы в одной зоне (точке) остаточных деформаций.
Заметные остаточные деформации в пластичных материалах появляются при напряжениях равных пределу текучести, отсюда следует, что для пластичных материалов предел текучести является предельным напряжением.
Хрупкие материалы разрушаются при малых пластических деформациях и для них предельным напряжением считают предел прочности
Напряжения предельные, допускаемые и расчетные.
Предельным напряжением считают напряжение, при котором в материале возникает опасное состояние (разрушение или опасная деформация).
Для пластичных материалов предельным напряжением считают предел текучести, т.к. возникающие пластические деформации не исчезают после снятия нагрузки:
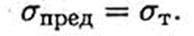
Для хрупких материалов, где пластические деформации отсутствуют, а разрушение возникает по хрупкому типу (шейки не образуется), за предельное напряжение принимают предел прочности:
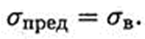
Для пластично-хрупких материалов предельным напряжением считают напряжение, соответствующее максимальной деформации 0,2% (сто,2):
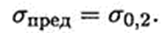
Допускаемое напряжение — максимальное напряжение, при котором материал должен нормально работать.
Допускаемые напряжения получают по предельным с учетом запаса прочности:
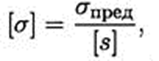
где [σ] — допускаемое напряжение; s — коэффициент запаса прочности; [s] — допускаемый коэффициент запаса прочности.
Примечание. В квадратных скобках принято обозначать допускаемое значение величины.
Допускаемый коэффициент запаса прочности зависит от качества материала, условий работы детали, назначения детали, точности обработки и расчета и т. д.
Он может колебаться от 1,25 для простых деталей до 12,5 для сложных деталей, работающих при переменных нагрузках в условиях ударов и вибраций.
Особенности поведения материалов при испытаниях на сжатие:
1. Пластичные материалы практически одинаково работают при растяжении и сжатии. Механические характеристики при растяжении и сжатии одинаковы.
2. Хрупкие материалы обычно обладают большей прочностью при сжатии, чем при растяжении: σвр < σвс.
Если допускаемое напряжение при растяжении и сжатии различно, их обозначают [σр] (растяжение), [σс] (сжатие).
Условие прочности.
Для решения вопроса о прочности, в соответствии с принятым методом расчёта на прочность по допускаемым напряжениям и условием прочности (1.4), запишем это условие применительно к растянутому (сжатому) стержню.
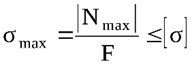
где |Nmax| – максимальная по абсолютному значению продольная сила;
F – площадь поперечного сечения стержня;
[σ] – допускаемое напряжение.
При решении задач сопротивления материалов [σ] всегда задано. При расчётах машин или конструкций Нормы расчёта дают указания по поводу назначения или расчёта [σ]. Формула (2.3) применима для стержня из материала, имеющего одинаковую прочность на растяжение и на сжатие (например, для стали). Но если материал по-разному сопротивляется растяжению и сжатию (например, чугун) для расчёта на прочность необходимо учитывать знак продольной силы и записывать два условия прочности
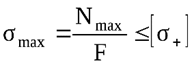 ,
, 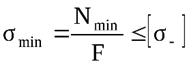
где Nmax – наибольшая (растягивающая) продольная сила;
Nmin – наименьшая (сжимающая) продольная сила;
[σ+] и [σ-] – допускаемые напряжения на растяжение и на сжатие соответственно.
Значение N, входящее в условие прочности, определяется предварительно по эпюреN(рис.2.3.) или из расчёта статического равновесия конструкции.
Рассмотрим пример. Необходимо определить размеры поперечного сечения стержней кронштейна, удерживающего нагрузку P= 100 кН (рис.2.6).
Стержень №1: стальной, круглый, [σ] = 160 МПа; стержень №2: деревянный, квадратный, [σ] = 12 МПа.
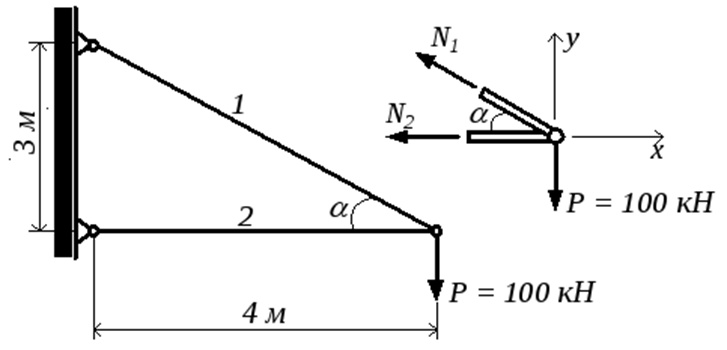
Рис.2.6
Сначала найдём усилия в стержнях. Для такой системы можно записать два уравнения статики:
∑ х = 0: – N2 – N1cos α = 0,
∑ y = 0: – P + N1sin α = 0.
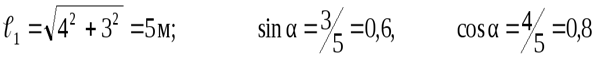
Из уравнения ∑ y = 0 найдём
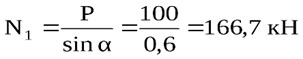
Из уравнения ∑ х = 0 найдём N2 = – N1cos α = – 166,7 ∙ 0,8 = – 133,3 кН.
Из условия прочности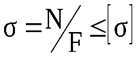
найдём площади поперечного сечения стержней
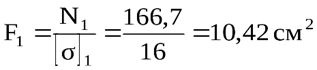 ,
, 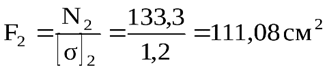
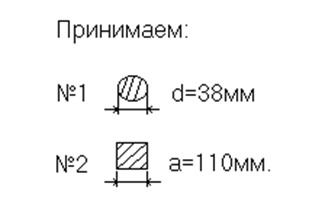
При расчётах прочности величину допускаемого напряжения, заданную в МПа, перевели в кН/см2: 160 МПа = 16 кН/см2 и 12 МПа = 1,2 кН/см2. Теперь осталось определить размеры поперечных сечений.
|
|
|
2.3. Деформации. Закон Гука
Рассмотрим деформации, возникающие при растяжении и сжатии стержней. При растяжении длина стержня увеличивается, а поперечные размеры сокращаются. При сжатии, наоборот, длина стержня уменьшается, а поперечные размеры увеличиваются. На рис.2.7 пунктиром показан деформированный вид растянутого стержня.

Рис.2.7
ℓ – длина стержня до приложения нагрузки;
ℓ1 – длина стержня после приложения нагрузки;
b – поперечный размер до приложения нагрузки;
b1 – поперечный размер после приложения нагрузки.
Абсолютная продольная деформация ∆ℓ = ℓ1 – ℓ.
Абсолютная поперечная деформация ∆b = b1 – b.
Значение относительной линейной деформации ε можно определить как отношение абсолютного удлинения ∆ℓ к первоначальной длине бруса ℓ
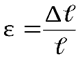
Аналогично находятся поперечные деформации
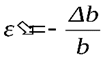
При растяжении поперечные размеры уменьшаются: ε > 0, ε′ < 0; при сжатии: ε < 0, ε′ > 0. Опыт показывает, что при упругих деформациях поперечная всегда прямо пропорциональна продольной.
ε′ = – νε. (2.7)
Коэффициент пропорциональности ν называется коэффициентом Пуассона или коэффициентом поперечной деформации. Он представляет собой абсолютную величину отношения поперечной деформации к продольной при осевом растяжении
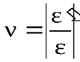
Назван по имени французского учёного, впервые предложившего его в начале XIX века. Коэффициент Пуассона есть величина постоянная для материала в пределах упругих деформаций (т.е. деформаций, исчезающих после снятия нагрузки). Для различных материалов коэффициент Пуассона изменяется в пределах 0 ≤ ν ≤ 0,5: для стали ν = 0,28…0,32; для резины ν = 0,5; для пробки ν = 0.
Между напряжениями и упругими деформациями существует зависимость, известная под названием закон Гука:
σ = Еε. (2.9)
Коэффициент пропорциональности Е между напряжением и деформацией называется модулем нормальной упругости или модулем Юнга. Размерность Е такая же, как и у напряжения. Так же, как и ν, Е – упругая постоянная материала. Чем больше значение Е, тем меньше, при прочих равных условиях, продольная деформация. Для стали Е = (2...2,2)105 МПа или Е = (2...2,2)104 кН/см2.
Подставляя в формулу (2.9) значение σ по формуле (2.2) и ε по формуле (2.5) , получим выражение для абсолютной деформации
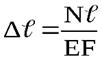
Произведение EF называется жёсткостью бруса при растяжении и сжатии.
Формулы (2.9) и (2.10) – это разные формы записи закона Гука, предложенного в середине XVII века. Современная форма записи этого фундаментального закона физики появилась гораздо позже – в начале XIX века.
Формула (2.10) справедлива лишь в пределах тех участков, где сила N и жёсткость EF постоянны. Для ступенчатого стержня и стержня, нагруженного несколькими силами, удлинения подсчитываются по участкам с постоянными N и F и результаты суммируются алгебраически
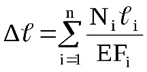
Если эти величины изменяются по непрерывному закону, ∆ℓ вычисляется по формуле
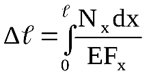
В ряде случаев для обеспечения нормальной работы машин и сооружений размеры их деталей должны быть выбраны так, чтобы кроме условия прочности обеспечивалось условие жёсткости
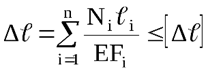
где ∆ℓ – изменение размеров детали;
[∆ℓ] – допускаемая величина этого изменения.
Подчёркиваем, что расчет на жёсткость всегда дополняет расчёт на прочность.
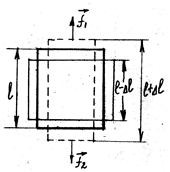
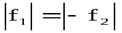 . Действие этих сил равномерно
распределено по всему сечению.
. Действие этих сил равномерно
распределено по всему сечению.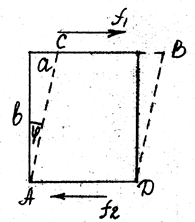
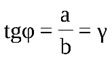 , если φ мал, то φ ≈ γ
, если φ мал, то φ ≈ γ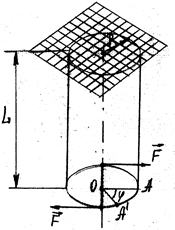
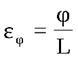 (3)
(3)